Espacio muestral.
El estudio de la estadística trata básicamente con la presentación e interpretación de resultados fortuitos que ocurren en un estudio planeado o en una investigación científica. El estadístico a menudo trata con datos experimentales, conteos o mediciones representativos, o quizá con datos categóricos que se podrían clasificar de acuerdo con algún criterio.
Nos referimos a cualquier registro de información, ya sea numérico o categórico, como una observación.
Los estadísticos utilizan la palabra experimento para describir cualquier proceso que genere un conjunto de datos.
El conjunto de todos los resultados posibles de un experimento estadístico se llama espacio muestral y se representa con el símbolo S. A cada resultado en un espacio muestral se le llama elemento o miembro del espacio muestral, o simplemente punto muestral. Si el espacio muestral tiene un número finito de elementos, podemos listar los miembros separados por comas y encerrarlos entre llaves. De esta forma, el espacio muestral S, de los resultados posibles cuando se lanza una moneda al aire, se escribe como S= {H,T} donde H y T corresponden a "caras" y "cruces", respectivamente.
Considere el experimento de lanzar un dado. Si nos interesamos en el núero que muestre en la cara superior, el espacio muestral sería S1= {1, 2, 3, 4, 5, 6}.
En algunos experimentos es útil listar los elementos del espacio muestral de forma sistemática utilizando un diagrama de árbol.
Nos referimos a cualquier registro de información, ya sea numérico o categórico, como una observación.
Los estadísticos utilizan la palabra experimento para describir cualquier proceso que genere un conjunto de datos.
El conjunto de todos los resultados posibles de un experimento estadístico se llama espacio muestral y se representa con el símbolo S. A cada resultado en un espacio muestral se le llama elemento o miembro del espacio muestral, o simplemente punto muestral. Si el espacio muestral tiene un número finito de elementos, podemos listar los miembros separados por comas y encerrarlos entre llaves. De esta forma, el espacio muestral S, de los resultados posibles cuando se lanza una moneda al aire, se escribe como S= {H,T} donde H y T corresponden a "caras" y "cruces", respectivamente.
Considere el experimento de lanzar un dado. Si nos interesamos en el núero que muestre en la cara superior, el espacio muestral sería S1= {1, 2, 3, 4, 5, 6}.
En algunos experimentos es útil listar los elementos del espacio muestral de forma sistemática utilizando un diagrama de árbol.
Experimento aleatorio
Es aquél que proporciona diferentes resultados aún y cuando se repita siempre de la misma manera.
¿Cuál es la probabilidad de que la suma de dos dados sea cinco?
S= {(1,4) , (2,3) , (3,2) , (4,1)}
4/36 = 1/9
Una caja contiene 3 pelotas: roja, azul y blanca. Dos de ellas se sacan con reemplazo. Esto implica:

S= {RR , RA , RB , AR , AA , AB , BR , BA , BB}
S= 9
Sin reemplazo:


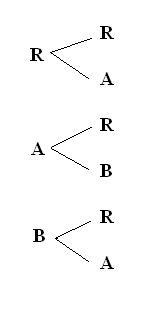
S= {RB , RA , AR , AB , BR , BA}
S= 6
¿Cuál es la probabilidad de que la suma de dos dados sea cinco?
S= {(1,4) , (2,3) , (3,2) , (4,1)}
4/36 = 1/9
Una caja contiene 3 pelotas: roja, azul y blanca. Dos de ellas se sacan con reemplazo. Esto implica:

S= {RR , RA , RB , AR , AA , AB , BR , BA , BB}
S= 9
Sin reemplazo:



S= {RB , RA , AR , AB , BR , BA}
S= 6
No hay comentarios:
Publicar un comentario