miércoles, 15 de octubre de 2008
martes, 14 de octubre de 2008
Teorema de Bayes
P(Ek|F) = P(F|Ek)P(Ek)/P(F)
Ejemplo: El software pra detectar fraudes en las tarjetas telefónicas registra todos los días el número de áreas metropolitanas donde se originan todas las llamadas. Se tiene que el 1% de los usuarios legítimos hace al día llamadas que se originan en 2 o más áreas metropolitanas. El 30% de los fraudulentos hacen al día llamadas desde dos o más áreas metropolitanas. La proporción de fraudulentos es 0.01%. Si el mismo usuario hace en un día dos o más llamadas desde dos o más áreas metropolitanas, ¿cuál es la probabilidad de que sea un usuario fraudulento?
1% usuarios legítimos hacen llamadas desde dos o más áreas metropolitanas.
30% usuarios fraudulentos hacen al día llamadas desde dos o más áreas metropolitanas.
Proporción de usuarios fraudulentos = 0.01%
A={usuario legítimo}
A'={usuario fraudulento}
B={llamada se origine en dos o más áreas}
P{usuario sea fraudulento}=0.0001
P{usuario sea legítimo}=1-0.0001=0.9999
P{B|A} = 0.01
P{B|A} = 0.3
P(A'|B) = P(B|A')P(A)/P(B) = P(B|A')P(A')/P(B|A)P(A) + P(B|A')P(A')
= (0.3)(0.0001)/(0.01)(0.999)+ (0.3)(0.0001) = 0.00299
Ejemplo: El software pra detectar fraudes en las tarjetas telefónicas registra todos los días el número de áreas metropolitanas donde se originan todas las llamadas. Se tiene que el 1% de los usuarios legítimos hace al día llamadas que se originan en 2 o más áreas metropolitanas. El 30% de los fraudulentos hacen al día llamadas desde dos o más áreas metropolitanas. La proporción de fraudulentos es 0.01%. Si el mismo usuario hace en un día dos o más llamadas desde dos o más áreas metropolitanas, ¿cuál es la probabilidad de que sea un usuario fraudulento?
1% usuarios legítimos hacen llamadas desde dos o más áreas metropolitanas.
30% usuarios fraudulentos hacen al día llamadas desde dos o más áreas metropolitanas.
Proporción de usuarios fraudulentos = 0.01%
A={usuario legítimo}
A'={usuario fraudulento}
B={llamada se origine en dos o más áreas}
P{usuario sea fraudulento}=0.0001
P{usuario sea legítimo}=1-0.0001=0.9999
P{B|A} = 0.01
P{B|A} = 0.3
P(A'|B) = P(B|A')P(A)/P(B) = P(B|A')P(A')/P(B|A)P(A) + P(B|A')P(A')
= (0.3)(0.0001)/(0.01)(0.999)+ (0.3)(0.0001) = 0.00299
Regla de la probabilidad
P {circuito integrado sujeto a altos niveles de contaminación sea la causa de una falla en un producto} = 0.10
P {circuito integrado que no está sujeto a altos niveles de contaminación sea la causa de la falla} = 0.005
20% de la producción está sujeta a altos niveles de contaminación.
¿Cuál es la probabilidad de que un producto que utilice alguno de estos circuitos falle?
A: {el circuito está expuesto a altos niveles de contaminación}
F: {el producto falla}
A':{el circuito no está expuesto a altos niveles de contaminación}

P(F|A) = 0.1
P(F|A') = 0.005
P(A) = 0.2
P(A') = 1-0.2 = 0.8
P(F) = P(F ∩ A) + P(F ∩ A')
P(F) = P(F|A)P(A) + P(F|A')P(A')
P(F) = (0.1)(0.2) + (0.005)(0.8)
P(F) = 0.024

Si se tiene más de dos eventos excluyentes entre sí:

P(F) = P(F ∩ E1) + P(F ∩ E2) + P(F ∩ E3) +.....+ P(F ∩ En)
P(F) = P(F|E1)P(E1) + P(F|E2)P(E2) + P(F|E3)P(E3) +.....+ P(F|En)P(En)
Ejemplo: La probabilidad de que falle un conector eléctrico durante el periodo de garantía es 1%. Si el conector se humedece la probabilidad de falla durante la garantía es 5%. Si el 90% de los conectores se mantienen secos y el 10% se humedece, ¿qué proporciones de los conectores fallará durante el periodo de garantía?
seco: P(F|E1) = 0.01, P(E1) = 0.9
húmedo: P(F|E2) = 0.05, P(E2) = 0.1
P(F) = P(F|E1)P(E1) + P(F|E2)P(E2)
P(F) = (0.01)(0.9) + (0.05)(0.1)
P(F) = O.014
P {circuito integrado que no está sujeto a altos niveles de contaminación sea la causa de la falla} = 0.005
20% de la producción está sujeta a altos niveles de contaminación.
¿Cuál es la probabilidad de que un producto que utilice alguno de estos circuitos falle?
A: {el circuito está expuesto a altos niveles de contaminación}
F: {el producto falla}
A':{el circuito no está expuesto a altos niveles de contaminación}

P(F|A) = 0.1
P(F|A') = 0.005
P(A) = 0.2
P(A') = 1-0.2 = 0.8
P(F) = P(F ∩ A) + P(F ∩ A')
P(F) = P(F|A)P(A) + P(F|A')P(A')
P(F) = (0.1)(0.2) + (0.005)(0.8)
P(F) = 0.024

Si se tiene más de dos eventos excluyentes entre sí:

P(F) = P(F ∩ E1) + P(F ∩ E2) + P(F ∩ E3) +.....+ P(F ∩ En)
P(F) = P(F|E1)P(E1) + P(F|E2)P(E2) + P(F|E3)P(E3) +.....+ P(F|En)P(En)
Ejemplo: La probabilidad de que falle un conector eléctrico durante el periodo de garantía es 1%. Si el conector se humedece la probabilidad de falla durante la garantía es 5%. Si el 90% de los conectores se mantienen secos y el 10% se humedece, ¿qué proporciones de los conectores fallará durante el periodo de garantía?
seco: P(F|E1) = 0.01, P(E1) = 0.9
húmedo: P(F|E2) = 0.05, P(E2) = 0.1
P(F) = P(F|E1)P(E1) + P(F|E2)P(E2)
P(F) = (0.01)(0.9) + (0.05)(0.1)
P(F) = O.014
Reglas multiplicativas
Si en un experimento pueden ocurrir los eventos A y B, entonces
P(A ∩ B) = P(A)P(B|A), dado que P(A)>0.
Así la probabilidad de que ocurran A y B es igual a la probabilidad de que ocurra A multiplicada por la probabilidad condicional de que ocurra B, dado que ocurre A.
Como los eventos A ∩ B y B ∩ a son equivalentes, del teorema anterior se sigue que también podemos escribir
P(A ∩ B) = P(B ∩ A) = P(B)P(A|B).
En otras palabras, no importa qué evento se considere como A y cuál como B.
Ejemplo: Suponga que tenemos una caja de fusibles que contiene 20 unidades, de las cuales 5 están defectuosas. Si se seleccionan 2 fusibles al azar y se retiran de la caja, uno después del otro, sin reemplazar el primero, ¿cuál es la probabilidad de que ambos fusibles estén defectuosos?
Sean A el evento de que el primer fusible esté defectuoso y B ele vento de que el segundo esté defectuoso; entonces, interpretamos A ∩ B como el evento de que ocurra A, y entonces B ocurre después de que haya ocurrido A. La probabilidad de separar primero un fusible defectuoso es 1/4; entonces, la probabilidad de separar un segundo fusible defectuoso de los restantes 4 es 4/19. Por lo tanto,
P(A ∩ B) = (1/4)(4/19) = 1/19.
Eventos independientes
Dos eventos A y B son independientes si y sólo si
P(A ∩ B) = P(A)P(B).
Por lo tanto, para obtener la probabilidad de que ocurran dos eventos independientes, simplemente calculamos el producto de sus probabilidades individuales.
P(A ∩ B) = P(A)P(B|A), dado que P(A)>0.
Así la probabilidad de que ocurran A y B es igual a la probabilidad de que ocurra A multiplicada por la probabilidad condicional de que ocurra B, dado que ocurre A.
Como los eventos A ∩ B y B ∩ a son equivalentes, del teorema anterior se sigue que también podemos escribir
P(A ∩ B) = P(B ∩ A) = P(B)P(A|B).
En otras palabras, no importa qué evento se considere como A y cuál como B.
Ejemplo: Suponga que tenemos una caja de fusibles que contiene 20 unidades, de las cuales 5 están defectuosas. Si se seleccionan 2 fusibles al azar y se retiran de la caja, uno después del otro, sin reemplazar el primero, ¿cuál es la probabilidad de que ambos fusibles estén defectuosos?
Sean A el evento de que el primer fusible esté defectuoso y B ele vento de que el segundo esté defectuoso; entonces, interpretamos A ∩ B como el evento de que ocurra A, y entonces B ocurre después de que haya ocurrido A. La probabilidad de separar primero un fusible defectuoso es 1/4; entonces, la probabilidad de separar un segundo fusible defectuoso de los restantes 4 es 4/19. Por lo tanto,
P(A ∩ B) = (1/4)(4/19) = 1/19.
Eventos independientes
Dos eventos A y B son independientes si y sólo si
P(A ∩ B) = P(A)P(B).
Por lo tanto, para obtener la probabilidad de que ocurran dos eventos independientes, simplemente calculamos el producto de sus probabilidades individuales.
Probabilidad condicional
La probabilidad de que un evento B ocurra cuando se sabe que ya ocurrió algún evento A se llama probabilidad condicional y se denota con P(B|A). El símbolo P(B|A), por lo general se lee "la probabilidad de que ocurra B dado que ocurrió A", o simplemente "la probabilidad de B, dado A".
La probabilidad condicional de B, dado A, que se denota con P(B|A), se define como
P(B|A) = P(A ∩ B)/P(A) si P(A)>0.
Ejemplo: La probabilidad de que un vuelo programado normalmente salga a tiempo es P(D) = 0.83; la probabilidad de que llegue a tiempo es P(A) = 0.82; y la probabilidad de que salga y llegue a tiempo es P(D ∩ A) = 0.78. Encuentre la probabilidad de que un avión
a)llegue a tiempo, dado que salió a tiempo;
y
b)salió a tiempo, dado que llegó a tiempo.
a)La probabilidad de que un avión llegue a tiempo, dado que salió a tiempo es
P(A|D) = P(D ∩ A)/P(D) = 0.78/0.83 = 0.94.
B)La probabilidad de que un avión haya salido a tiempo, dado que llegó a tiempo es
P(D|A) = P(D ∩ A)/P(A) = 0.78/0.82 = 0.95.
Eventos independientes
Dos eventos A y B son independientes si y sólo si
P(B|A) = P(B) O P(A|B) = P(A)
dada la existencia de probabilidad condicional. De otra forma, A y B son dependientes.
La probabilidad condicional de B, dado A, que se denota con P(B|A), se define como
P(B|A) = P(A ∩ B)/P(A) si P(A)>0.
Ejemplo: La probabilidad de que un vuelo programado normalmente salga a tiempo es P(D) = 0.83; la probabilidad de que llegue a tiempo es P(A) = 0.82; y la probabilidad de que salga y llegue a tiempo es P(D ∩ A) = 0.78. Encuentre la probabilidad de que un avión
a)llegue a tiempo, dado que salió a tiempo;
y
b)salió a tiempo, dado que llegó a tiempo.
a)La probabilidad de que un avión llegue a tiempo, dado que salió a tiempo es
P(A|D) = P(D ∩ A)/P(D) = 0.78/0.83 = 0.94.
B)La probabilidad de que un avión haya salido a tiempo, dado que llegó a tiempo es
P(D|A) = P(D ∩ A)/P(A) = 0.78/0.82 = 0.95.
Eventos independientes
Dos eventos A y B son independientes si y sólo si
P(B|A) = P(B) O P(A|B) = P(A)
dada la existencia de probabilidad condicional. De otra forma, A y B son dependientes.
Reglas aditivas
Si A y B son dos eventos, entonces
P(A U B) = P(A) + P(B) - P(A ∩ B).
Ejemplo: Al final del semestre, Juan se va a graduar en la facultad de ingeniería industrial en una universidad. Después de tener entrevistas en dos compañías donde quiere trabajar, él evalúa la probabilidad que tiene de lograr una oferta de empleo en la compañía A como 0.8, y la probabilidad de obtenerla de la compañia B como 0.6. Si, por otro lado, considera que la probabilidad de que reciba ofertas de ambas compañías es 0.5, ¿cuál es la probabilidad de que obtendrá al menos una oferta de esas dos compañías?
Con la regla aditiva tenemos: P(A U B) = P(A) + P(B) - P(A ∩ B)=
0.8 + 0.6 - 0.5 = 0.9.
P(A U B) = P(A) + P(B) - P(A ∩ B).

Ejemplo: Al final del semestre, Juan se va a graduar en la facultad de ingeniería industrial en una universidad. Después de tener entrevistas en dos compañías donde quiere trabajar, él evalúa la probabilidad que tiene de lograr una oferta de empleo en la compañía A como 0.8, y la probabilidad de obtenerla de la compañia B como 0.6. Si, por otro lado, considera que la probabilidad de que reciba ofertas de ambas compañías es 0.5, ¿cuál es la probabilidad de que obtendrá al menos una oferta de esas dos compañías?
Con la regla aditiva tenemos: P(A U B) = P(A) + P(B) - P(A ∩ B)=
0.8 + 0.6 - 0.5 = 0.9.
Probabilidad de un evento
La probabilidad de un evento A es la suma de los pedos de todos los puntos muestrales en A. Por lo tanto,
0 <= P(A) <= 1 , P(ø) = 0 y P(S) = 1
Además, si A1, A2, A3, ... es una serie de eventos mutuamente excluyentes, entonces
P1(A1 U A2 U A3 U ... ) = P(A1) + P(A2) + P(A3) + ...
Ejemplo: Sea A el evento de que salga un número par y sea B el evento de que salga un número divisible entre 3. Encuentre P(A U B) y P(A ∩ B).
Para los eventos A = {2, 3, 4, 6} y B = {3, 6}, tenemos
Para los eventos A = {2, 3, 4, 6} y B = {3, 6}, tenemos
A U B = {2, 3, 4, 6} y A ∩ B = {6}.
Si un experimento puede tener como resultado cualquiera de N diferentes resultados dos igualmente probables, y si exactamente n de estos resultados corresponden al evento A, entonces la probabilidad del evento A es
Al asignar una probabilidad de 1/9 a cada número non y de 2/9 a cada número par, tenemos
P(A U B) = 2/9 + 1/9 + 2/9 + 2/9 = 7/9 y P(A ∩ B) = 2/9
Si un experimento puede tener como resultado cualquiera de N diferentes resultados dos igualmente probables, y si exactamente n de estos resultados corresponden al evento A, entonces la probabilidad del evento A es
P(A) = n/N
Ejemplo: Una clase de estadística para ingenieros consta de 25 estudiantes de ingeniería industrial, 10 de mecánica, 10 de eléctrica y 8 de civil. Si el profesor elige a una persona al azar para que conteste una pregunta, encuentre la probabilidad de que el estudiante elegido sea
a) un estudiante de ingeniería industrial
b) uno que de ingeniería civil o eléctrica
Se denotan con I, M, E y C las especialidades de ingenierías. El número total de estudiantes en la clase es 53, todos los cuales tienen la misma probabilidad de ser seleccionados.
a) Como 25 de los 53 estudiantes tienen la especialidad de ingeniería industrial, la probabilidad del evento I, elegir al azar a alguien de ingeniería industrial es
a) un estudiante de ingeniería industrial
b) uno que de ingeniería civil o eléctrica
Se denotan con I, M, E y C las especialidades de ingenierías. El número total de estudiantes en la clase es 53, todos los cuales tienen la misma probabilidad de ser seleccionados.
a) Como 25 de los 53 estudiantes tienen la especialidad de ingeniería industrial, la probabilidad del evento I, elegir al azar a alguien de ingeniería industrial es
P(I) = 25/53
b) como 18 de los 53 estudiantes son de las especialidades de ingeniería civil o eléctrica, se sigue que
P(C U E) = 18/53
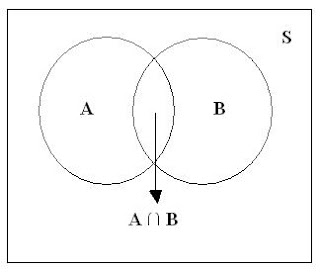
Diagrama de Venn
La relación entre eventos y el correspondiente espacio muestral se puede ilustrar de forma gráfica utilizando diagramas de Venn. en un diagrama de Venn representamos el espacio muestral como un rectángulo y los eventos con círculos trazados dentro del rectángulo.
En la figura vemos que:

A ∩ B = regiones 1 y 2,
B ∩ C = regiones 1 y 3,
A U C = regiones 1, 2, 3, 4, 5 y 7,
B' ∩ A = regiones 4 y 7,
A ∩ B ∩ C = región 1,
(A U B) ∩ C' = regiones 2, 6 y 7,
y así sucesivamente.
Ls figura puede representar una situación donde seleccionamos una carta al azar de una baraja ordinaria de 52 cartas y observamos si ocurren los siguientes eventos:
A: la carta es roja,
B: la carta es el jack, la reina o el rey de diamantes,
C: la carta es un as.
El evento A ∩ C consiste sólo en los dos ases rojos.
Varios resultados que se derivan de las definiciones procedentes, y que se pueden verificar de forma sencilla empleando diagramas de Venn, son los que siguen:
A ∩ ø = ø
A U ø = A
A ∩ A' = ø
A U A' = S
S' = ø
ø' = S
(A')' = A
(A ∩ B)' = A U B
(A U B )' = A' ∩ B'
En la figura vemos que:

A ∩ B = regiones 1 y 2,
B ∩ C = regiones 1 y 3,
A U C = regiones 1, 2, 3, 4, 5 y 7,
B' ∩ A = regiones 4 y 7,
A ∩ B ∩ C = región 1,
(A U B) ∩ C' = regiones 2, 6 y 7,
y así sucesivamente.
Ls figura puede representar una situación donde seleccionamos una carta al azar de una baraja ordinaria de 52 cartas y observamos si ocurren los siguientes eventos:
A: la carta es roja,
B: la carta es el jack, la reina o el rey de diamantes,
C: la carta es un as.
El evento A ∩ C consiste sólo en los dos ases rojos.
Varios resultados que se derivan de las definiciones procedentes, y que se pueden verificar de forma sencilla empleando diagramas de Venn, son los que siguen:
A ∩ ø = ø
A U ø = A
A ∩ A' = ø
A U A' = S
S' = ø
ø' = S
(A')' = A
(A ∩ B)' = A U B
(A U B )' = A' ∩ B'
lunes, 13 de octubre de 2008
Eventos
Para cada evento asignamos una colección de puntos muestrales, que constituye un subconjunto del espacio muestral. Ese subconjunto representa la totalidad de los elementos para los que el evento es cierto.
Ejemplo: Dado el espacio muestral S= {t|t>=0}, donde t es la vida en años de cierto componente electrónico, entonces el evento A de que el componente falle antes de que finalice el quinto año es el subconjunto A= {t|0<=t<=5}.
Es concebible que un evento sea un subconjunto que incluya todo el espacio muestral S, o un subconjunto de S que se denomina conjunto vacío y se denota con el símbolo ø, que no contiene elemento alguno.
El complemento de un evento A respecto de S es el subconjunto de todos los elemntos de S que no están en A. Denotamos el complemento de A mediante el símbolo A'.
Ejemplo: Sea R el evento de que se seleccione una carta roja de una baraja ordinaria de 52 cartas, y sea S toda la baraja. Entonces, R' es el evento de que la carta seleccionada de la baraja no sea una roja sino una negra.
La intersección de dos eventos A y B, que se denota con el símbolo A ∩ B, es el evento que contiene todos los elementos que son comunes a A y a B.
Ejemplo: Sea C el evento de que una persona seleccionada al azar en un café Internet sea un estudiante universitario, y sea M el evento de que la persona sea hombre. Entonces C ∩ M es el evento de todos los estidiantes universitarios hombres en el café Internet.
Ejemplo: Sean M = {a, e, i, o, u} y N = {r, s, t}; entonces, se sigue que M ∩ N = ø. Es decir, M y N no tienen elementos comunesy, por lo tanto, no pueden ocurrir ambos de forma simultánea.
Dos eventos A y B son mutuamente excluyentes o disjuntos si A ∩ B = ø; es decir, si A y B no tienen elementos en común.
La unión de dos eventos A y B, que se denota con el símbolo A U B, es el evento que contiene todos los elementos que pertenecen a A o a B o a ambos.
Ejemplo: Sea A = {a, b, a} y B = {b, c, d, e}, entonces A U B = {a, b, c, d, e}. Sea P el evento de que un empleado seleccionado al azar de una compañía petrolera fume cigarrillos. Sea Q el evento de que el empleado seleccionado ingiera bebidas alcohólicas. Entonces, el evento P U Q es el conjunto de todos los empleados que beben o fuman, o que hacen ambas cosas.
Si M = {x | 3 < n =" {y" n =" {z">
Ejemplo: Dado el espacio muestral S= {t|t>=0}, donde t es la vida en años de cierto componente electrónico, entonces el evento A de que el componente falle antes de que finalice el quinto año es el subconjunto A= {t|0<=t<=5}.
Es concebible que un evento sea un subconjunto que incluya todo el espacio muestral S, o un subconjunto de S que se denomina conjunto vacío y se denota con el símbolo ø, que no contiene elemento alguno.
El complemento de un evento A respecto de S es el subconjunto de todos los elemntos de S que no están en A. Denotamos el complemento de A mediante el símbolo A'.
Ejemplo: Sea R el evento de que se seleccione una carta roja de una baraja ordinaria de 52 cartas, y sea S toda la baraja. Entonces, R' es el evento de que la carta seleccionada de la baraja no sea una roja sino una negra.
La intersección de dos eventos A y B, que se denota con el símbolo A ∩ B, es el evento que contiene todos los elementos que son comunes a A y a B.
Ejemplo: Sea C el evento de que una persona seleccionada al azar en un café Internet sea un estudiante universitario, y sea M el evento de que la persona sea hombre. Entonces C ∩ M es el evento de todos los estidiantes universitarios hombres en el café Internet.
Ejemplo: Sean M = {a, e, i, o, u} y N = {r, s, t}; entonces, se sigue que M ∩ N = ø. Es decir, M y N no tienen elementos comunesy, por lo tanto, no pueden ocurrir ambos de forma simultánea.
Dos eventos A y B son mutuamente excluyentes o disjuntos si A ∩ B = ø; es decir, si A y B no tienen elementos en común.
La unión de dos eventos A y B, que se denota con el símbolo A U B, es el evento que contiene todos los elementos que pertenecen a A o a B o a ambos.
Ejemplo: Sea A = {a, b, a} y B = {b, c, d, e}, entonces A U B = {a, b, c, d, e}. Sea P el evento de que un empleado seleccionado al azar de una compañía petrolera fume cigarrillos. Sea Q el evento de que el empleado seleccionado ingiera bebidas alcohólicas. Entonces, el evento P U Q es el conjunto de todos los empleados que beben o fuman, o que hacen ambas cosas.
Si M = {x | 3 < n =" {y" n =" {z">
UNIDAD II. PROBABILIDAD
Espacio muestral.
El estudio de la estadística trata básicamente con la presentación e interpretación de resultados fortuitos que ocurren en un estudio planeado o en una investigación científica. El estadístico a menudo trata con datos experimentales, conteos o mediciones representativos, o quizá con datos categóricos que se podrían clasificar de acuerdo con algún criterio.
Nos referimos a cualquier registro de información, ya sea numérico o categórico, como una observación.
Los estadísticos utilizan la palabra experimento para describir cualquier proceso que genere un conjunto de datos.
El conjunto de todos los resultados posibles de un experimento estadístico se llama espacio muestral y se representa con el símbolo S. A cada resultado en un espacio muestral se le llama elemento o miembro del espacio muestral, o simplemente punto muestral. Si el espacio muestral tiene un número finito de elementos, podemos listar los miembros separados por comas y encerrarlos entre llaves. De esta forma, el espacio muestral S, de los resultados posibles cuando se lanza una moneda al aire, se escribe como S= {H,T} donde H y T corresponden a "caras" y "cruces", respectivamente.
Considere el experimento de lanzar un dado. Si nos interesamos en el núero que muestre en la cara superior, el espacio muestral sería S1= {1, 2, 3, 4, 5, 6}.
En algunos experimentos es útil listar los elementos del espacio muestral de forma sistemática utilizando un diagrama de árbol.
Nos referimos a cualquier registro de información, ya sea numérico o categórico, como una observación.
Los estadísticos utilizan la palabra experimento para describir cualquier proceso que genere un conjunto de datos.
El conjunto de todos los resultados posibles de un experimento estadístico se llama espacio muestral y se representa con el símbolo S. A cada resultado en un espacio muestral se le llama elemento o miembro del espacio muestral, o simplemente punto muestral. Si el espacio muestral tiene un número finito de elementos, podemos listar los miembros separados por comas y encerrarlos entre llaves. De esta forma, el espacio muestral S, de los resultados posibles cuando se lanza una moneda al aire, se escribe como S= {H,T} donde H y T corresponden a "caras" y "cruces", respectivamente.
Considere el experimento de lanzar un dado. Si nos interesamos en el núero que muestre en la cara superior, el espacio muestral sería S1= {1, 2, 3, 4, 5, 6}.
En algunos experimentos es útil listar los elementos del espacio muestral de forma sistemática utilizando un diagrama de árbol.
Experimento aleatorio
Es aquél que proporciona diferentes resultados aún y cuando se repita siempre de la misma manera.
¿Cuál es la probabilidad de que la suma de dos dados sea cinco?
S= {(1,4) , (2,3) , (3,2) , (4,1)}
4/36 = 1/9
Una caja contiene 3 pelotas: roja, azul y blanca. Dos de ellas se sacan con reemplazo. Esto implica:

S= {RR , RA , RB , AR , AA , AB , BR , BA , BB}
S= 9
Sin reemplazo:


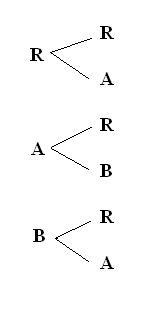
S= {RB , RA , AR , AB , BR , BA}
S= 6
¿Cuál es la probabilidad de que la suma de dos dados sea cinco?
S= {(1,4) , (2,3) , (3,2) , (4,1)}
4/36 = 1/9
Una caja contiene 3 pelotas: roja, azul y blanca. Dos de ellas se sacan con reemplazo. Esto implica:

S= {RR , RA , RB , AR , AA , AB , BR , BA , BB}
S= 9
Sin reemplazo:



S= {RB , RA , AR , AB , BR , BA}
S= 6
martes, 7 de octubre de 2008
lunes, 6 de octubre de 2008
Diagrama de tallo y hoja
El tallo está formado por uno o más de los dígitos principales y una hoja la cual contiene el resto de los dígitos. En general debe escogerse un número relativamente pequeño de tallos en comparación con el número de observaciones. Lo usual es seleccionar entre 5 y 20 tallos.
Construcción de la gráfica
Para hacer la gráfica primero se necesita tener la tabla de datos agrupados. Ya que se tiene se hacen las dos líneas como las azules en la figura. Se puede utilizar escala, en este caso es de 1 cm.

La línea de la izquierda representa la frecuencia y la de abajo representan los datos, empezando de la esquina, cada línea son los límites que se muestran en la tabla de datos agrupados. Se construyen las barras basándose en la frecuencia de la tabla, para cada intervalo. Con las puras barras sería una gráfica de barras o un HISTOGRAMA. Ahora ubicamos las marcas de clase, o puntos medios entre cada intervalo y se unen, empezando desde la esquina inferior izquierda, y terminando en la esquina inferior derecha. Ahora tenemos un POLIGONO DE FRECUENCIAS y se pueden borrar las barras y que queden solo las líneas.

domingo, 5 de octubre de 2008
Datos Agrupados
Se refiera a una distribución de frecuencias
Construcción de una tabla de frecuencias:
(Tomando en cuenta los datos de la tabla enterior):
1.- Definir el rango = Vmaz - Vmin
2.- Cálculo de clase
a) número de clases =
b) ancho de clase =
3.- Intervalos de clase

Construcción de una tabla de frecuencias:
(Tomando en cuenta los datos de la tabla enterior):
1.- Definir el rango = Vmaz - Vmin
2.- Cálculo de clase
a) número de clases =
b) ancho de clase =
3.- Intervalos de clase
| Intervalos | Frec. | M.C. | (frec)(m.c.) |
| 95 < x <> | 2 | 110 | 220 |
| 125 < x <> | 6 | 140 | 840 |
| 155 < x <> | 8 | 170 | 1360 |
| 185 < x <> | 5 | 200 | 1000 |
| 215 < x <> | 4 | 230 | 920 |
| | 30 | | 4340 |
Suscribirse a:
Entradas (Atom)