La función de probabilidad de X puede interpretarse como la proporción de ensayos en los que X=x. En consecuencia, en realidad no es necesario realizar el experimento muchas veces con la finalidad de determinar el valor medio de X. La media de X puede calcularse como el promedio ponderado de los valores posibles de X, asignando al resultado x un factor de ponderación fx(x)= P(X=x).
La media de X puede interpretarse como el centro de la masa del rango de los valores de X. Esto es, si se coloca una masa igual a fx(x) en cada punto x de la recta real, entonces E(X) es el punto donde la recta queda en equilibrio. Por consiguiente, el término "función de probabilidad" puede interpretarse mediante esta analogía con la mecánica.
M = E(X)= Σ xi f(xi)
Ejemplo: Se supone que la cobertura de una prueba en el proceso de verificación de un semiconductor tiene una eficacia del 80%. Esto es, la probabilidad de que un chip defectuoso no pase la prueba es 0.8. Se someten a prueba tres chip. Supóngase que la falla en cada chip defectuoso es independiente de las que aparezcan en otras pruebas. Sea la variable aleatoria X el número de chips defectuosos que no pasan la prueba. ¿Cuál es el valor esperado de X'?
Para hallar E(X) primero es necesario encontrar la función de probabilidad de X. La tabla siguiente presenta los resultados posibles de este experimento junto con los valores correspondientes de X. La probabilidad de cada resultado se obtiene con ayuda de la hipótesis de independencia. En la tabla, p indica que el chip pasa la prueba, y f, que el chip no pasa la prueba (falle). Por tanto, el resultado donde el primer chip pasa la prueba y los demás no, se denota por ppf. Por oitra parte, P(ppf)= 0.2 x 0.8 x 0.8 = 0.128.
X - {número de chips que no pasan la prueba}

Gráfica de distribución de frecuencias:
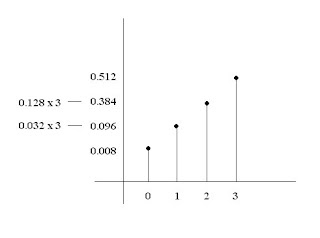
La función de probabilidad de X se encuentra a partir de estos resultados.

M = 0(0.008) + 1(0.096) + 2(0.384) + 3(0.512) = 2.4
No hay comentarios:
Publicar un comentario