Distribución Uniforme DiscretaUna variable aleatoria X es una variable aleatoria discreta uniforme si cada uno de los n valores que están en el rango de ésta, x1, x2,....., xn, tiene la misma probabilidad. Entonces,
fx(x)= 1/n
Ejemplo: La probabilidad de que el primer dígito del número de serie de una pieza sea uno de los números desde 0 hasta 9, es la misma. Si se toma una pieza al azar de un lote muy grande, y X es el primer dígito del número de serie, entonces X tiene una distribución discreta uniforme con una probabilidad 0.1 para cada valor de R = {0,1,2,...,9}. Esto es, fx(x)= 0.1 para cada valor de R.
Función de probabilidad de X:
 Distribución Discreta Binomial
Distribución Discreta BinomialTipos de experimentos que utilizan una función binomial: Ensayo de Bernoulli.
Ensayo de Bernoulli: Un experimento en el que se pueden presentar n ensayos repetidos tales que:
1)Los ensayos son independientes.
2)Cada ensayo tiene solo dos resultados posibles denominados "éxito" y "fracao".
3)La probabilidad de éxito de cada ensayo, denotada por p, permanece constante.
Ejemplo: La posibilidad de recibir de manera errónea un bit transmitido por un canal de transmisión digital, es 0.1. Además, supóngase que los ensayos de transmisión son independientes. Sea X = número de bits recibidos con error en los próximos cuatro que serán transmitidos. Descríbase el espacio muestral de este experimento e indíquese el valor de X en cada resultado. Calcúlese P(X=2).
En este experimento se indica con E un bit erróneo, y con C un bit sin error, esto es, recibido correctamente. Con esto, el espacio muestral de este experimento puede describirse como una lista de cuatro letras que indican qué bits fueron recibidos con y sin error. Por ejemplo, el resultado CECE indica que el segundo y el cuarto bit son erróneos, y los otros dos se recibieron correctamente. Por consiguiente, el espacio muestral es:
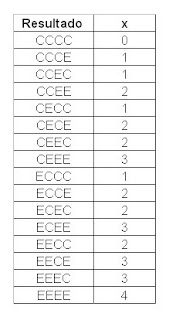
Funciones de probabilidad:
P(X=0)= (0.656)1
P(X=1)= (0.0729)4
P(X=2)= (0.0081)6
P(X=3)= (0.0009)4
P(X=4)= (0.0001)1
 Combinaciones:
Combinaciones:
Entonces:
 Distribución Binomial:
Distribución Binomial:


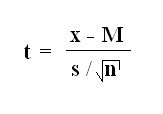


.bmp)
.bmp)
.bmp)













