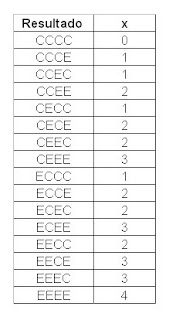
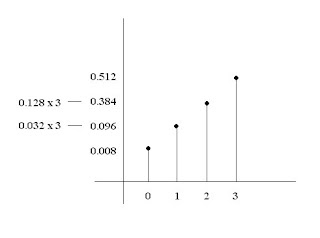
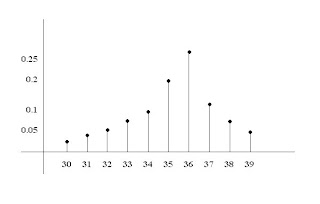
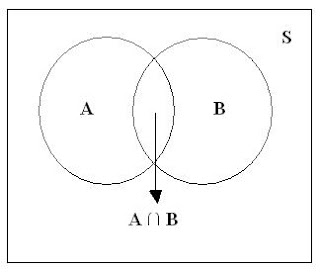
Para cada evento asignamos una colección de puntos muestrales, que constituye un subconjunto del espacio muestral. Ese subconjunto representa la totalidad de los elementos para los que el evento es cierto.
Ejemplo: Dado el espacio muestral S= {t|t>=0}, donde t es la vida en años de cierto componente electrónico, entonces el evento A de que el componente falle antes de que finalice el quinto año es el subconjunto A= {t|0<=t<=5}.
Es concebible que un evento sea un subconjunto que incluya todo el espacio muestral S, o un subconjunto de S que se denomina conjunto vacío y se denota con el símbolo ø, que no contiene elemento alguno.
El complemento de un evento A respecto de S es el subconjunto de todos los elemntos de S que no están en A. Denotamos el complemento de A mediante el símbolo A'.
Ejemplo: Sea R el evento de que se seleccione una carta roja de una baraja ordinaria de 52 cartas, y sea S toda la baraja. Entonces, R' es el evento de que la carta seleccionada de la baraja no sea una roja sino una negra.
La intersección de dos eventos A y B, que se denota con el símbolo A ∩ B, es el evento que contiene todos los elementos que son comunes a A y a B.
Ejemplo: Sea C el evento de que una persona seleccionada al azar en un café Internet sea un estudiante universitario, y sea M el evento de que la persona sea hombre. Entonces C ∩ M es el evento de todos los estidiantes universitarios hombres en el café Internet.
Ejemplo: Sean M = {a, e, i, o, u} y N = {r, s, t}; entonces, se sigue que M ∩ N = ø. Es decir, M y N no tienen elementos comunesy, por lo tanto, no pueden ocurrir ambos de forma simultánea.
Dos eventos A y B son mutuamente excluyentes o disjuntos si A ∩ B = ø; es decir, si A y B no tienen elementos en común.
La unión de dos eventos A y B, que se denota con el símbolo A U B, es el evento que contiene todos los elementos que pertenecen a A o a B o a ambos.
Ejemplo: Sea A = {a, b, a} y B = {b, c, d, e}, entonces A U B = {a, b, c, d, e}. Sea P el evento de que un empleado seleccionado al azar de una compañía petrolera fume cigarrillos. Sea Q el evento de que el empleado seleccionado ingiera bebidas alcohólicas. Entonces, el evento P U Q es el conjunto de todos los empleados que beben o fuman, o que hacen ambas cosas.
Si M = {x | 3 < n =" {y" n =" {z">

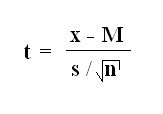


.bmp)
.bmp)
.bmp)